ГЛОСАРІЙ
Специальные | А | Б | В | Г | Д | Е | Ё | Ж | З | И | К | Л | М | Н | О | П | Р | С | Т | У | Ф | Х | Ц | Ч | Ш | Щ | Э | Ю | Я | Все
А |
|---|
Алгебрарозділ математики, що вивчає властивості дій над різноманітними величинами і розв’язки рівнянь, пов’язаних з цими діями. | ||
Арифметика(від
грецького arithmos – число) – наука, що вивчає дії над цілими числами, вчить
розв’язувати задачі, які зводяться до додавання, віднімання, множення і ділення
цих чисел. | ||
Арифметичний коріньневід’ємне
число , n-а
степінь якого дорівнює невід’ємному числу а. | |
Б |
|---|
Біквадратне рівняннярівняння четвертого степеня виду ax4 +bx2 +c=0, де а≠0 | |
В |
|---|
Вієта теорема
| |
Д |
|---|
Дискримінант тричленаякщо тричлен має вигляд р(х)= ax2 + bx + c, то D = b2 – 4ac. | |
І |
|---|
Ірраціональні числа(позначення для множини — | |
К |
|---|
Квадратне рівнянняалгебраїчне рівняння другого степеня; загальне кавдратне рівняння з одним невідомим х має вигляд: ax2+bx+c=0 де a, b, c – дійсні числа, причому а≠0. В дійсних числах квадратне рівняння може мати один, два корені або не мати дійсних коренів. | |
Корінь рівняннярозв’язок рівняння, значення невідомого, яке перетворює дане рівняння з одним невідомим в тотожність. | |
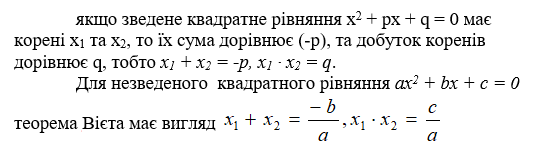
 ) — це всі
) — це всі  , — тобто не можуть бути записані як
, — тобто не можуть бути записані як  ,
,  , ,
, ,  ), а лише нескінченними неперіодичними
), а лише нескінченними неперіодичними